Lab 8: Stunt

Stunt Chosen and Implementation

I chose to do the flip stunt, where I drive forward at full speed, then quickly reverse to flip the back of my car forward. I chose this because of two main reasons:

1. This can be done mostly open-loop, so there would be a lot less trouble tuning PID parameters for angle.
2. The success of the flip can be greatly modified by the car’s weight distribution. My robot already has a lot of weight on the front, so if I just added a little more weight further up, I already have the setup for a successful flip.

To implement this, I built a bluetooth command to start the stunt, and another to retrieve the data from the filter. Before fleshing out the function, I needed to plan out where I would store my data. In my code, I have two array sizes, called array_size and pid_array_size. pid_array_size is larger, and would easily be able to fit my Kalman filter data. The following things are what need to be stored, and the solution I picked:

1. Time array (TOF) -> global array timestamp_array, defined in Lab 2
2. Distance array (TOF) -> global array distance1_array, defined in Lab 3
3. Time array (KF) -> NEW global array big_timestamp_array of size pid_array_size
4. Distance array (KF) -> use Kalman filter’s internal KF.distance_array, defined in Lab 7

With that sorted, I wrote the following bluetooth code, factoring out the main logic into another function for clarity.

case START_STUNT:
{
  // Globals
  stunt_tof_index = 0;
  stunt_kf_index = 0;
  
  //TOF and slower timestamp array
  for (int i = 0; i < array_size; i++){
    timestamp_array[i] = 0;
    distance1_array[i] = 0;
  }

  //KF timestamp array
  for (int i = 0; i < pid_array_size; i++){
    big_timestamp_array[i] = 0;
  }

  // Initialize with first measurement, for Kalman filter to work
  // NOTE: getTof1IfReady() returns -1.0 if data is not available.
  float d1 = getTof1IfReady();
  while (d1 == -1.0){
    delay(5);
    Serial.println("START_STUNT: WAITING FOR FIRST TOF DATA");
    d1 = getTof1IfReady();
  }
  pos_kf.initialize(d1);
  
  stunt_start_time = millis();
  timestamp_array[stunt_tof_index] = stunt_start_time;
  distance1_array[stunt_tof_index] = d1;
  stunt_tof_index++;

  // Call stunt function.
  stuntOpenLoop();

  // Just to make sure we stop after stunt is over.
  stop();
  break;
}

The main function, stuntOpenLoop(), runs through all of the necessary logic to complete the flip. First, it drives at full speed against the wall. After it reaches a certain threshold (determined through trial and error) from its Kalman filter prediction of state, the car jumps into reverse and drives for a predetermined amount of time (then it’s up to me or the wall to stop it!).

void stuntOpenLoop()
{
const float flipDistance = 1200; // mm
const float maxRunTime = 10000;  // ms

// 1. Start by driving forward against the wall by default.
drive(FORWARD, 255);

// 2. Initialize and run Kalman filter. Stay in the loop until we reach threshold
float d1 = getTof1IfReady();
while (1)
{
  unsigned long cur_time = millis();

  if (d1 != -1.0)
  {
    timestamp_array[stunt_tof_index] = cur_time;
    distance1_array[stunt_tof_index] = d1;
    stunt_tof_index++;

    pos_kf.update(d1);
  }
  // Note this stores to pos_kf's array for distance.
  // Also note negation, see lab 7.
  pos_kf.predict(KalmanFilter::normalize(-255));

  float cur_pos = pos_kf.getPosition();
  big_timestamp_array[stunt_kf_index] = cur_time;
  pos_kf.position_array[stunt_kf_index] = cur_pos;
  stunt_kf_index++;

  if (cur_pos < flipDistance || cur_time - stunt_start_time > maxRunTime)
  {
    break; // out of the while loop
  }

  d1 = getTof1IfReady();
}
}

To fetch the data, I simply loop over all of the arrays described above. All the unused array elements are post-processed in Python by filtering out zeros.

case FETCH_D1:
{
  for (int i = 0; i < array_size; i++){
    tx_estring_value.clear();
    tx_estring_value.append("T:");
    tx_estring_value.append(timestamp_array[i]);
    tx_estring_value.append("|");
    tx_estring_value.append("P:");
    tx_estring_value.append(distance1_array[i]);
    tx_characteristic_string.writeValue(tx_estring_value.c_str());
  }
  break;
}

case FETCH_STUNT_KF:
{
  for (int i = 0; i < pid_array_size; i++){
    tx_estring_value.clear();
    tx_estring_value.append("T:");
    tx_estring_value.append(big_timestamp_array[i]);
    tx_estring_value.append("|");
    tx_estring_value.append("P:");
    tx_estring_value.append(pos_kf.position_array[i]);
    tx_characteristic_string.writeValue(tx_estring_value.c_str());
  }
  break;
}

One thing to note is that I changed the Kalman filter variances to be lower than in Lab 7 so that the velocity would be more conservative, but I’m not sure if it made any difference in the end.

//KalmanFilter pos_kf(dt, mass, dist, sigma_meas, sigma_proc_1, sigma_proc_2);
// sigma_proc = sqrt(20^2 * 10) = 63.24
// sigma_proc = sqrt(10^2 * 10) = 31.62
// in mm units
KalmanFilter pos_kf(0.00856, 0.000258, 0.000339, 20, 31.62, 31.62);

The Results

I ran the code until 3 successful trials, each of which are given below, with the video, distance graph, and motor input (even though it’s just 255 and -225). Unfortunately I didn’t time the results, but it seems like Trial 3 is the fastest? It looks to be ~2.5 to 3 seconds from the YouTube playback bar.

Trial 1:

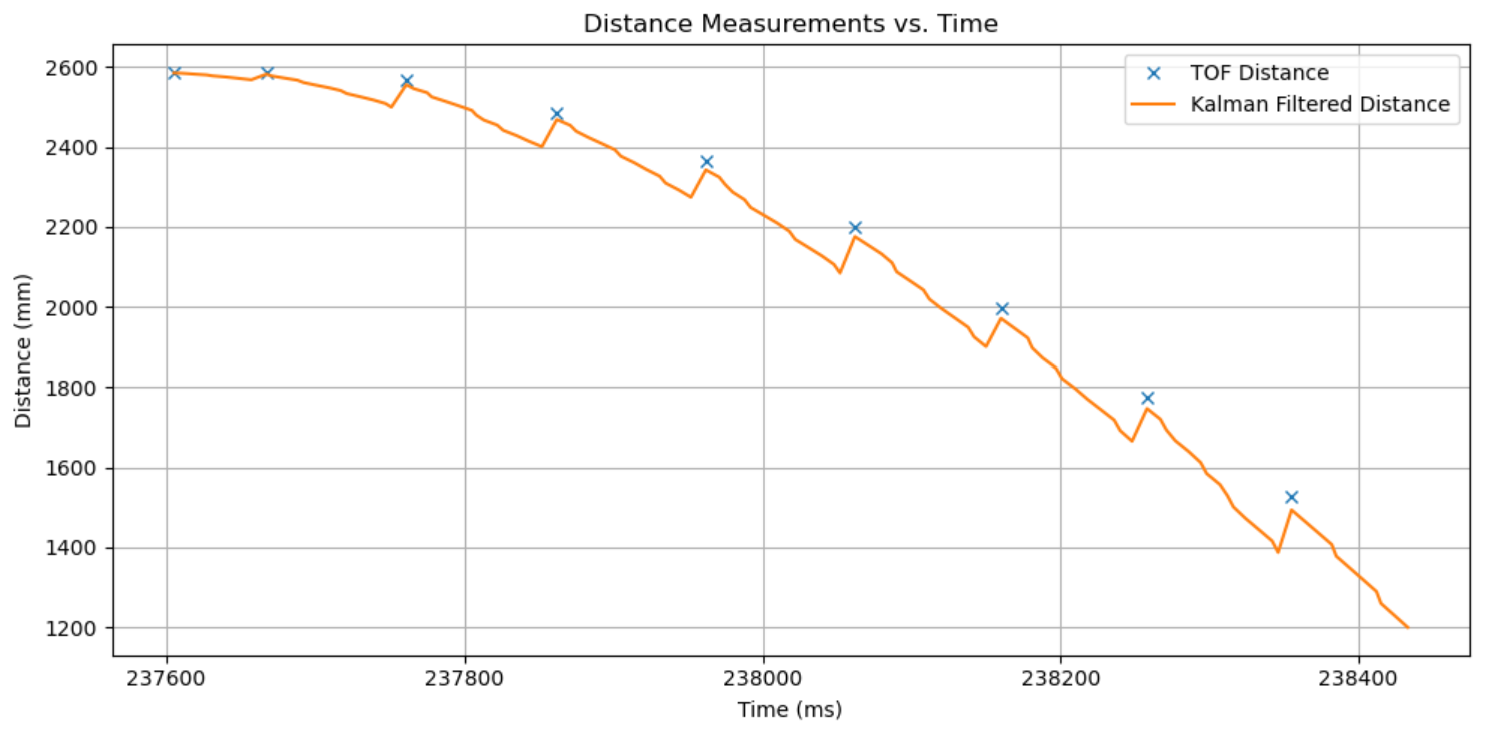
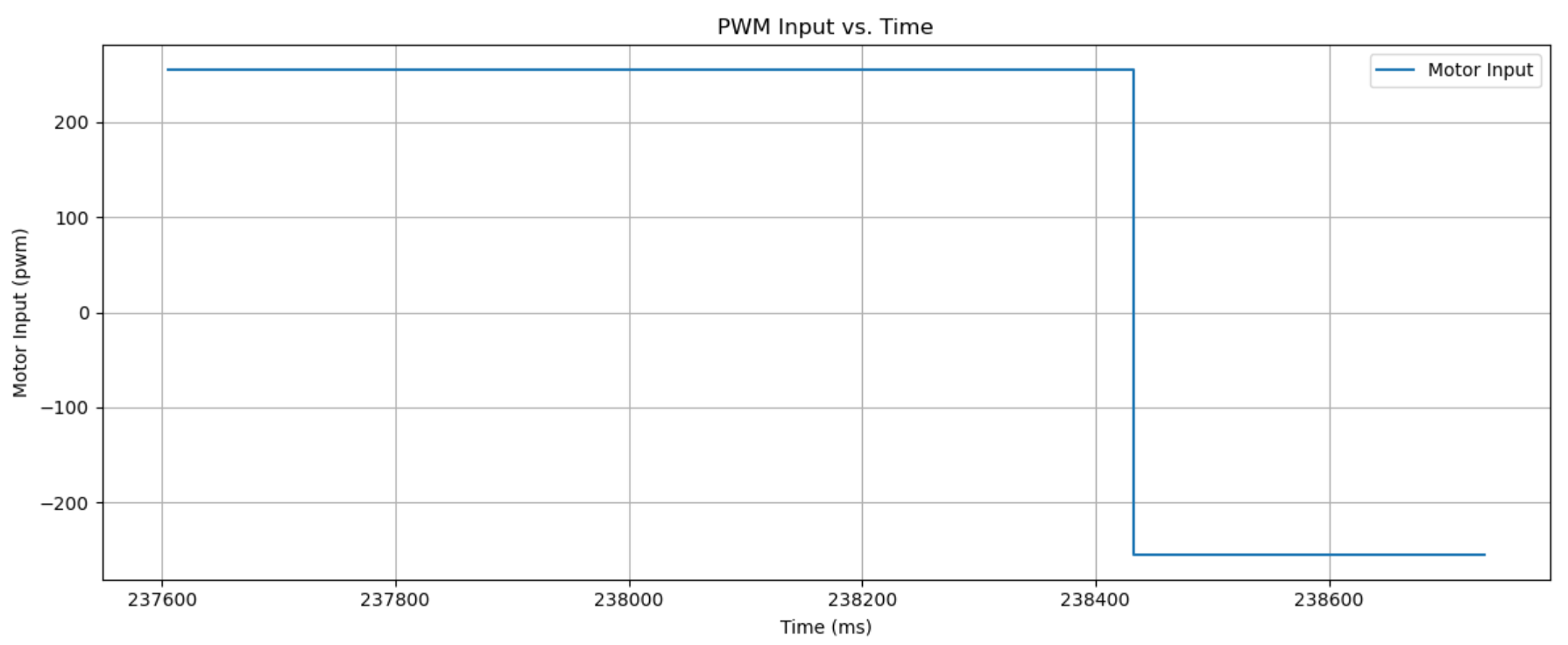
Trial 2:

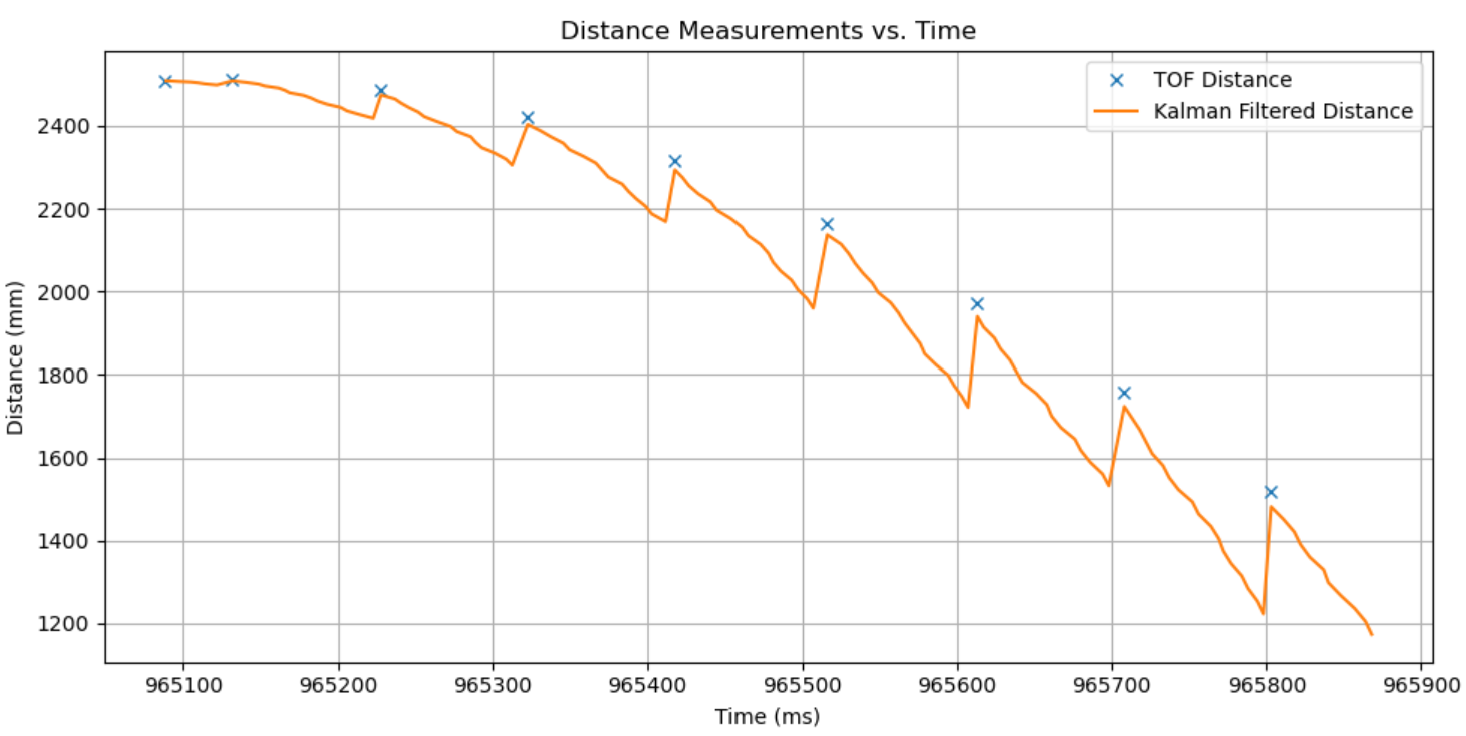
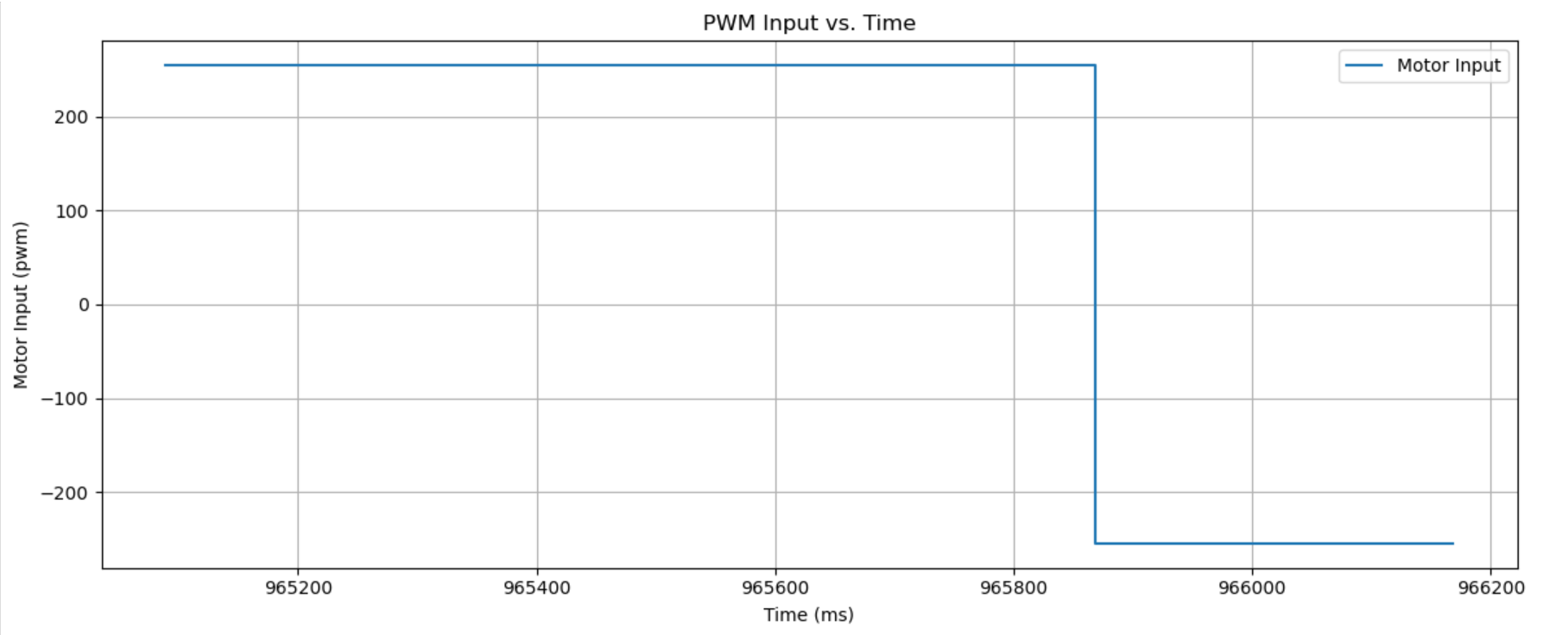
Trial 3:

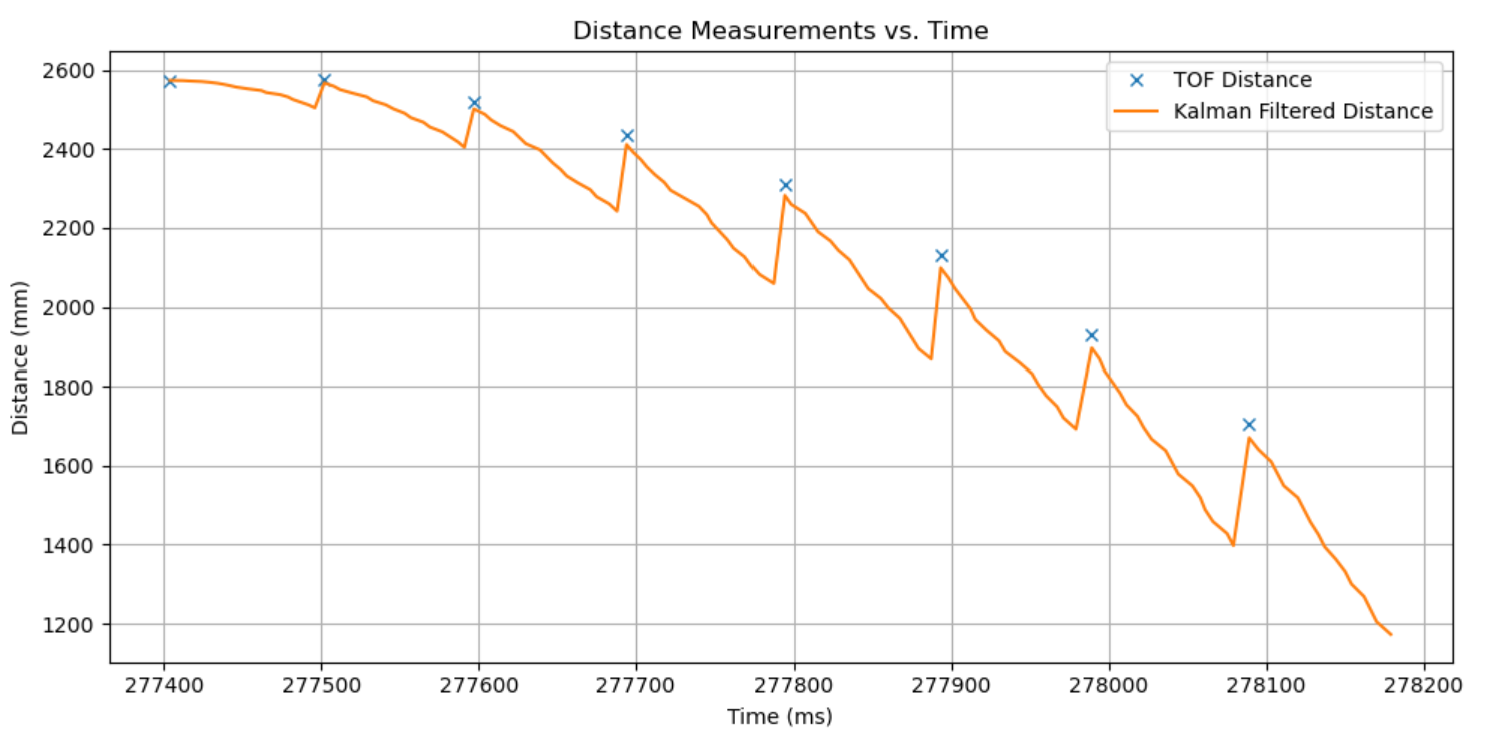
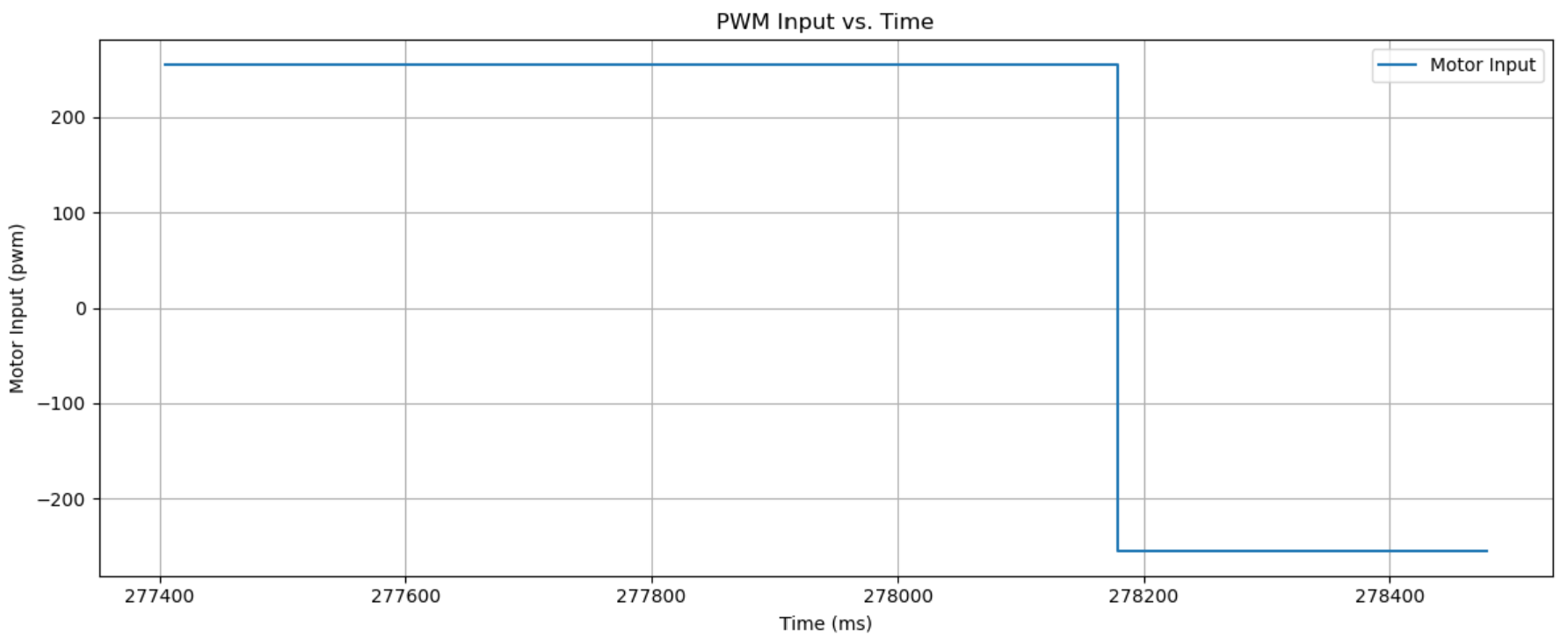
Blooper

Sometimes, my robot didn’t want to cooperate! To mock my inanimate robot, I made a stupid video of it. Enjoy!

Acknowledgements

• Thanks to Lucca for giving me a weight pack for the stunt! Also his website is really nice and you should look at it.
• Thanks to Farrell for sanity checking my weight distribution!